
A avaliação da capabilidade de processo representa um dos pilares da engenharia da qualidade e da gestão industrial orientada por dados. A capacidade de transformar requisitos de especificação em desempenho mensurável exige compreensão profunda dos mecanismos estatísticos que governam a variabilidade, da relação entre limites técnicos e comportamento real do processo, e da influência das condições operacionais e organizacionais sobre a repetibilidade e a estabilidade. A construção de indicadores como Cp, Cpk, Pp e Ppk não se resume ao cálculo matemático, mas envolve a análise crítica da distribuição dos dados, da maturidade dos controles aplicados, da robustez dos sistemas produtivos e do alinhamento entre desempenho observado e resultados que precisam ser sustentados ao longo do tempo. A indústria utiliza esses índices para avaliar riscos, projetar melhorias, priorizar intervenções, estabelecer critérios de aceitação e conduzir decisões com impacto direto em custos, produtividade, confiabilidade e desempenho regulatório. A compreensão aprofundada dessas métricas exige interpretação integrada entre estatística, processos, engenharia, garantia da qualidade, tomada de decisão gerencial e melhoria contínua.
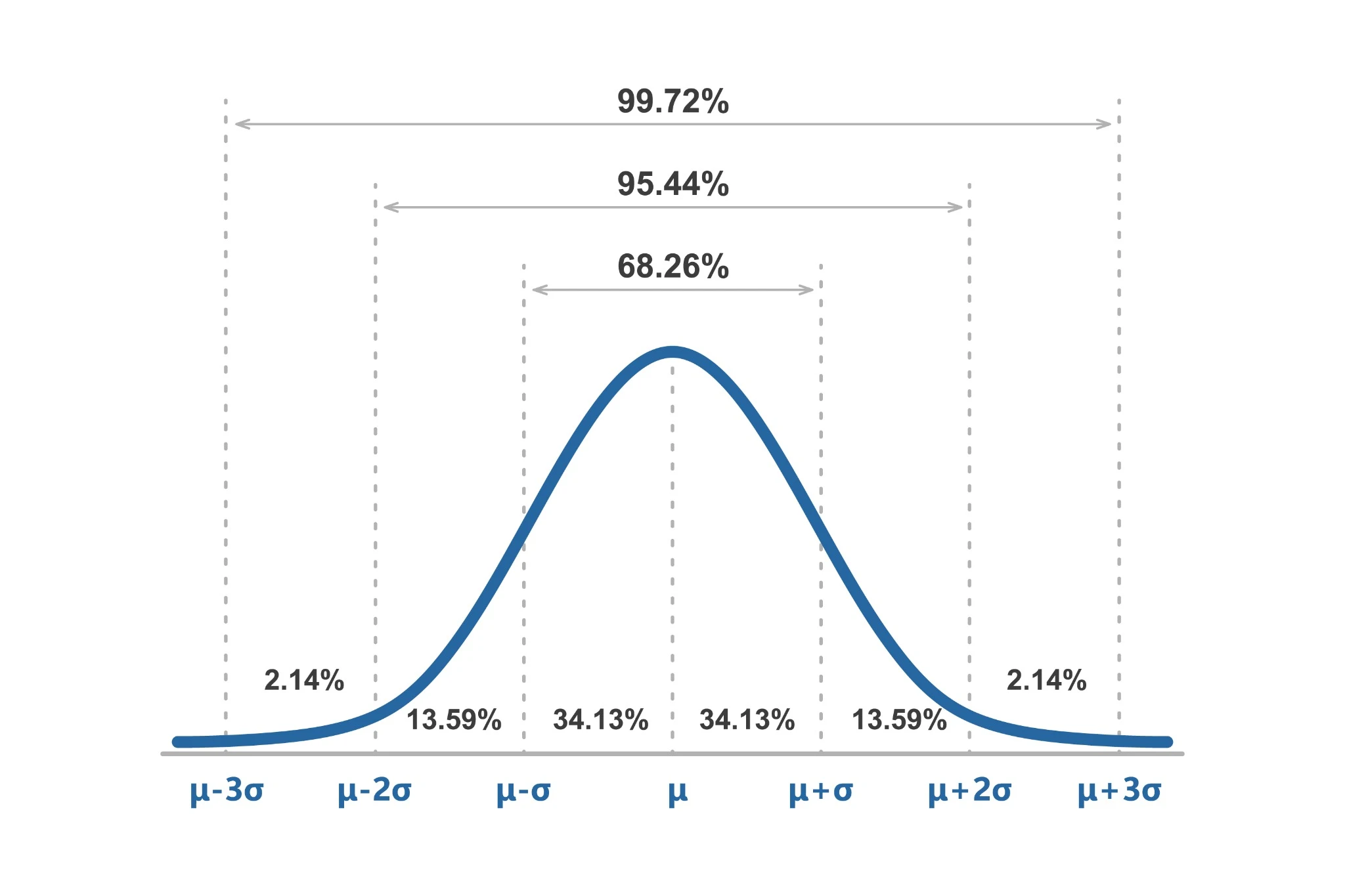
A base conceitual da capabilidade de processo depende da compreensão de como a variação influencia a conformidade. Todo processo apresenta dispersão natural resultante de fatores intrínsecos ao sistema, como características de máquinas, comportamento de matéria-prima, ambiente, operadores e métodos de operação. Essa variabilidade pode ser considerada inerente ao processo quando os fatores que a geram permanecem estáveis ao longo do tempo, demonstrando comportamento previsível e repetível. A mensuração dessa variabilidade parte da suposição de que os dados seguem distribuição aproximadamente normal, o que permite estimar probabilidades de eventos fora dos limites de especificação. Quando a distribuição é compatível com o modelo estatístico, o desvio padrão se torna o parâmetro central para avaliar o espaçamento entre o desempenho e os limites definidos pelo cliente ou pela engenharia. O conceito de capabilidade surge exatamente da comparação entre a amplitude da especificação e a amplitude da variabilidade real. Quanto maior a distância entre os limites e a dispersão dos dados, maior a probabilidade de conformidade. Quando essa distância diminui, o risco de produto fora da especificação aumenta e o processo exige ajustes, controles adicionais ou reavaliação das condições de operação.
A relação entre especificação e desempenho real não é estática. Mudanças sutis nas condições industriais podem alterar a variabilidade ou a média do processo. A capabilidade traduz o quanto o processo consegue atender consistentemente as necessidades impostas. Esse entendimento é essencial porque muitos profissionais concentram a análise apenas na média, ignorando a dispersão. Um processo perfeitamente centrado, mas com variabilidade elevada, pode produzir grande volume de itens fora do limite. Por outro lado, um processo com variabilidade baixa, mas deslocado do centro, também pode gerar falhas se não houver controle adequado. A capabilidade integra esses dois aspectos, demonstrando a condição real do processo frente às exigências técnicas.
A distinção entre comportamento de curto prazo e longo prazo é fundamental para compreender como Cp, Cpk, Pp e Ppk devem ser aplicados. O curto prazo representa a condição em que a variabilidade observada é essencialmente inerente ao processo, ou seja, livre de causas especiais e fenômenos externos que introduzem flutuações adicionais. Esse cenário idealizado utiliza o desvio padrão dentro dos subgrupos para refletir o comportamento puro do sistema. É nesse contexto que se calculam Cp e Cpk, que medem a capacidade potencial do processo de atender os limites de especificação. Esses índices assumem que o processo está sob controle estatístico e que as causas de variação são estritamente relacionadas a fatores comuns.
O longo prazo representa o comportamento que incorpora todas as fontes de variação que ocorrem ao longo do ciclo operacional real. Oscilações de turnos, variações ambientais, mudanças de operadores, ajustes de máquinas, desgaste de ferramentas, diferenças entre lotes de matéria-prima e alterações programadas ou não programadas têm impacto direto sobre o desempenho global. Esse conjunto de fatores aumenta a variabilidade total e reduz a capacidade de atender especificações com consistência. Pp e Ppk utilizam o desvio padrão global, calculado com base em toda a população de dados sem segmentação em subgrupos. Isso faz com que Pp e Ppk representem o desempenho efetivo e não apenas o potencial.
A diferença entre curto e longo prazo é decisiva para análises gerenciais. Cp e Cpk são adequados quando se deseja compreender o limite máximo de desempenho possível caso o processo fosse totalmente estável. Pp e Ppk refletem a realidade do chão de fábrica, incluindo mudanças operacionais e interferências que fazem parte das condições práticas de produção. A interpretação correta exige a integração dessas duas visões para identificar lacunas entre potencial e desempenho real, permitindo compreender se o processo tem falhas de controle, se precisa de padronização, se há oportunidades de melhoria ou se é necessário reavaliar métodos de operação.
O índice Cp representa a razão entre a largura da especificação e a largura da distribuição estatística do processo em condições de curto prazo. É calculado pela fórmula clássica que relaciona os limites superior e inferior de especificação ao desvio padrão estimado dentro dos subgrupos. O pressuposto central é a estabilidade, pois Cp só é válido quando o processo apresenta comportamento estatisticamente controlado. Quando essa condição é violada, o índice deixa de ser representativo. O valor de Cp indica o potencial máximo de atendimento às especificações independentemente do posicionamento da média. Isso significa que um processo pode apresentar Cp elevado e ainda assim gerar não conformidades caso esteja descentralizado. Por esse motivo, Cp é sempre interpretado em conjunto com Cpk.
Cpk incorpora o deslocamento da média em relação aos limites. Sua fórmula avalia o quão distante o centro do processo está dos limites, considerando a dispersão interna. Um processo centrado terá valores iguais para as duas componentes do cálculo de Cpk, enquanto um processo deslocado terá uma das margens reduzida. Valores baixos de Cpk indicam risco elevado de não conformidade, independentemente da magnitude de Cp. Essa distinção é essencial na engenharia de processos porque Cp avalia apenas a largura da variabilidade, enquanto Cpk mede a posição da média. Um processo com baixa variação mas média deslocada pode ser incapaz de atender requisitos. Outro processo, com média centralizada mas variação elevada, também apresenta risco significativo. A combinação dos índices permite entender se o problema é variabilidade ou centragem.
A interpretação técnica exige análise integrada com dados reais do processo, gráficos de controle e histórico operacional. Cpk inferior a 1 geralmente indica incapacidade. Valores próximos a 1 implicam operação no limite, com risco elevado. Valores acima de 1,33 são frequentemente usados em critérios industriais para aceitação de processos, enquanto níveis acima de 1,67 refletem operação robusta e repetível. Esses valores não devem ser interpretados de forma isolada, pois certas indústrias exigem índices superiores devido a requisitos críticos de qualidade. A análise deve considerar risco associado, impacto regulatório, custo de falhas e maturidade dos controles aplicados.
O comportamento da média e do desvio padrão determina diretamente os valores de Cp e Cpk. Quando a média se desloca em direção a um dos limites, a margem disponível para absorver a variabilidade diminui, reduzindo o valor de Cpk. Esse deslocamento pode ocorrer por mudanças de setup, variações ambientais, desgaste de ferramentas, deriva de equipamentos, alterações de lote de matéria-prima ou diferenças de método. A variabilidade, representada pelo desvio padrão de curto prazo, também exerce papel central. Quando o processo é mais disperso, mesmo que a média esteja centrada, a capacidade de atender os limites diminui.
O alinhamento entre média, limites e dispersão precisa ser interpretado sob perspectiva operacional. Em processos críticos, pequenas variações têm impacto elevado. A análise da centragem deve sempre ser acompanhada da avaliação de causas potenciais de deslocamento, como procedimentos inadequados, falta de padronização, treinamento insuficiente ou ausência de manutenção preventiva. A interpretação integrada permite avançar da simples compreensão estatística para a gestão ativa da capabilidade, transformando números em ações de controle e melhoria contínua.
Pp e Ppk utilizam o desvio padrão global para representar o comportamento real ao longo do tempo, incluindo oscilações naturais e variações não controladas. Enquanto Cp e Cpk refletem potencial teórico, Pp e Ppk traduzem a prática industrial. Essa diferença se torna evidente quando processos apresentam variações entre turnos, ajustes constantes de máquina ou interferência de fatores externos. Quando o desvio padrão global é maior que o desvio padrão dentro dos subgrupos, Pp e Ppk tendem a ser significativamente menores que Cp e Cpk. Essa diferença indica ausência de estabilidade e reforça a necessidade de investigação.
A compreensão dessa relação é determinante para a melhoria contínua. Quando Cp é alto, mas Pp é baixo, o processo tem potencial, mas não tem controle. Quando ambos são baixos, o processo é incapaz, independentemente da abordagem. Quando Cp e Cpk são similares a Pp e Ppk, o processo é estável e previsível, representando condição ideal para gestão industrial. A comparação direta dos quatro índices funciona como diagnóstico integrado de estabilidade, centragem e variabilidade, indicando o caminho de investigação e melhoria a ser seguido.
A instabilidade altera significativamente a interpretação dos índices. Variações introduzidas por lotes, operadores, setups ou manutenção criam um cenário em que a variabilidade global ultrapassa a capacidade do processo de produzir dentro da especificação. Em ambientes industriais complexos, a instabilidade pode estar associada a fatores como desgaste de componentes críticos, variações térmicas, inadequação de procedimentos ou ausência de controles robustos. Quando a instabilidade é elevada, Ppk se torna o indicador mais representativo do risco real, permitindo compreender a probabilidade efetiva de falhas.
A análise da variabilidade real deve considerar tendências, ciclos operacionais e mudanças graduais que podem ser mascaradas pela média. A abordagem completa envolve segmentação dos dados, avaliação de fontes de variação, análise de causas especiais e compreensão das interações entre fatores de processo. A melhoria contínua depende de compreender não apenas o valor numérico dos índices, mas a estrutura que os sustenta.
A estabilidade é pré-requisito absoluto para o cálculo e interpretação de Cp e Cpk, e representa um dos pilares fundamentais da estatística aplicada à gestão da qualidade. A definição de estabilidade envolve a demonstração de que o processo opera apenas sob a influência de causas comuns, sem interferência de causas especiais que alterem o comportamento estatístico ao longo do tempo. Essa avaliação parte da construção de gráficos de controle que utilizam subgrupos racionais para separar variações inerentes daquelas introduzidas por eventos imprevisíveis. A utilização de gráficos Xbarra-R, Xbarra-S, I-MR ou alternativas equivalentes depende da natureza dos dados, do tamanho do subgrupo e da frequência de amostragem. A análise dessas cartas permite identificar padrões como pontos fora dos limites, instabilidade cíclica, tendências contínuas, alternância sistemática entre valores altos e baixos, agrupamentos atípicos ou comportamentos que violam os pressupostos do controle estatístico. Cada um desses padrões indica presença de causas especiais, como ajustes inadequados de máquina, mudanças de operador, variações de matéria-prima, falhas de equipamento ou erros de medição.
Além da avaliação de estabilidade, a verificação da normalidade é igualmente essencial, pois a maior parte das fórmulas clássicas de capabilidade assume distribuição aproximadamente normal. Essa verificação utiliza testes estatísticos, como Anderson-Darling ou Shapiro-Wilk, combinados com gráficos de probabilidade normal, histogramas e densidade estimada. A avaliação de normalidade não é binária; ela inclui julgamento técnico baseado na experiência industrial, no tamanho da amostra e na sensibilidade do processo a pequenas variações. Muitas situações industriais apresentam desvios discretos da normalidade que não comprometem a aplicação dos índices, desde que se reconheçam limitações e se interpretem resultados com prudência. A análise integrada de estabilidade e normalidade representa um filtro técnico que previne o cálculo indevido de Cp e Cpk, que seriam incorretos caso o processo não opere sob variabilidade puramente comum.
A análise de tendências complementa essa abordagem ao identificar mudanças graduais no processo que podem ainda estar dentro dos limites, mas que, ao longo do tempo, alteram significativamente o comportamento global. Equipamentos que sofrem desgaste, reagentes que perdem propriedades, dispositivos de medição que perdem calibração e operadores que mudam práticas ao longo do turno são exemplos clássicos de fatores que produzem deriva gradual. Esse movimento altera a centragem e, quando não detectado, compromete tanto o curto prazo quanto o longo prazo. A verificação de tendências usa gráficos de controle, séries temporais, regressão e segmentações por período. A análise de estabilidade exige olhar refinado sobre dados, conhecimento do processo e interpretação crítica apoiada por engenharia e estatística.
Calcular capabilidade sem avaliar estabilidade resulta em conclusões incorretas que distorcem decisões gerenciais e operacionais. Um dos erros mais frequentes ocorre quando se utiliza Cp e Cpk para processos que apresentam fortes variações externas ou internas. Nesses casos, o desvio padrão dentro dos subgrupos é menor que o desvio padrão global, criando falsa impressão de alta capacidade. Essa interpretação equivocada leva gestores a acreditar que o processo opera dentro de parâmetros aceitáveis quando, na realidade, variações entre turnos ou ciclos operacionais ampliam significativamente o risco de não conformidade. Outro erro frequente ocorre ao ignorar a presença de causas especiais, como ajustes esporádicos, falhas em sensores ou alterações não documentadas em procedimentos. Essas situações reduzem a previsibilidade, tornam os dados incompatíveis com o modelo estatístico e eliminam a possibilidade de confiar nos índices.
Outro equívoco comum envolve interpretar distribuições assimétricas como instabilidade, quando na verdade essas distribuições podem ser estáveis, porém naturalmente não normais. Processos industriais que lidam com tempos de reação, viscosidade, dissolução, pressões ou qualquer variável com limites físicos tendem a produzir assimetria, especialmente quando operam próximos a limites naturais. Interpretações equivocadas podem levar a conclusões incorretas sobre estabilidade quando o que se precisa é avaliar modelos alternativos, como transformações ou métodos não paramétricos. A avaliação adequada da estabilidade elimina erros de interpretação, evita decisões inadequadas e cria base sólida para cálculo preciso dos índices.
A utilização de amostras pequenas para cálculo da capabilidade também compromete a interpretação. Amostras insuficientes reduzem a confiabilidade estatística dos estimadores e geram flutuações artificiais que podem indicar falsamente incapacidade ou capacidade excessiva. A falta de padronização no método de coleta também afeta estabilidade. Mudanças de operador, horários distintos de coleta, alterações de equipamento e inconsistência na periodicidade produzem variabilidade artificial que não representa verdadeiramente o comportamento do processo. Esses erros se tornam ainda mais relevantes em ambientes de alta complexidade industrial, onde decisões com impacto financeiro significativo são tomadas com base em análises de capabilidade.
O cálculo correto de Cp, Cpk, Pp e Ppk exige disciplina estatística e compreensão profunda das equações envolvidas. O ponto de partida é a definição dos limites de especificação que determinam a janela de conformidade desejada pela engenharia ou pelo cliente. Em seguida, define-se o conjunto de dados coletados em condições apropriadas, respeitando critérios de estabilidade e representatividade. Para Cp, utiliza-se o desvio padrão de curto prazo, estimado pelo método das amplitudes médias ou pela média dos desvios padrão dos subgrupos, dependendo da carta de controle utilizada. O cálculo de Cp utiliza a diferença entre limite superior e limite inferior dividida por seis vezes o desvio padrão de curto prazo. Esse valor reflete quantas vezes a distribuição cabe dentro da especificação.
O cálculo de Cpk agrega à fórmula elementos de centragem. A interpretação requer avaliar duas situações: a distância da média ao limite superior e a distância da média ao limite inferior. Ambas as distâncias são convertidas em unidades de desvio padrão e o menor valor representa o Cpk. Quando a média está exatamente no centro da especificação, Cpk será igual a Cp. Quando há deslocamento, Cpk diminui proporcionalmente à magnitude desse deslocamento. Esse cálculo representa o risco de o processo atingir um dos limites e demonstra a combinação crítica entre variabilidade e centragem.
O cálculo de Pp utiliza o desvio padrão global. A fórmula substitui o desvio padrão de curto prazo pelo desvio padrão calculado diretamente sobre toda a população de dados. Esse cálculo incorpora variações de longo prazo, resultando em valores menores em processos instáveis. Pp demonstra quantas vezes a distribuição global se encaixa nos limites. O cálculo de Ppk repete a lógica de Cpk, porém utilizando o desvio padrão global. A interpretação representa o desempenho real, considerando todos os fatores que afetam o processo ao longo do tempo.
A interpretação dos índices depende do contexto industrial e do risco associado ao processo. Em processos de manufatura discreta, Cp e Cpk elevados sugerem capacidade consistente de produzir peças dentro da especificação, desde que a estabilidade seja comprovada. Em processos contínuos, variações pequenas são amplificadas ao longo do ciclo de produção, tornando indispensável a avaliação crítica de tendências e deriva gradual. Quando Cp e Cpk são elevados, mas Pp e Ppk são significativamente menores, o processo apresenta potencial, mas não apresenta controle adequado. Esse cenário exige investigação sobre variabilidade entre turnos, ajustes inadequados, deterioração de equipamentos ou falhas de padronização.
Quando todos os índices são baixos, o processo apresenta desempenho insuficiente e demanda melhorias estruturais. Isso pode incluir revisão de parâmetros operacionais, análise de matérias-primas, implementação de padronização ou reengenharia de equipamentos. Em ambientes regulatórios, como indústrias farmacêuticas, alimentícias ou químicas, índices elevados não apenas demonstram conformidade, mas também representam evidência de robustez para inspeções e auditorias. Em processos automotivos ou aeronáuticos, valores de capabilidade são frequentemente utilizados como critérios contratuais, determinando aceitação de fornecedores e definição de tolerâncias.
Quando o processo apresenta Cpk muito menor que Cp, o problema é centragem. Quando Ppk é muito menor que Cpk, o problema é instabilidade. Quando ambos são baixos, a variabilidade é excessiva e o processo é incapaz. Essas interpretações orientam a tomada de decisão com precisão, permitindo priorizar intervenções e focar em causas reais de problemas.
A construção de curvas de capabilidade complementa o cálculo dos índices ao fornecer visualização gráfica da relação entre distribuição dos dados e limites de especificação. O histograma demonstra a frequência relativa dos valores e evidencia assimetrias, multimodalidades, dispersão e deslocamentos. A curva de densidade estimada, sobreposta ao histograma, permite interpretar o formato da distribuição e avaliar compatibilidade com modelos estatísticos. A interpretação visual complementa a análise matemática, fornecendo evidências adicionais sobre adequação ou inadequação dos índices de capabilidade.
O cálculo do Z-score oferece perspectiva adicional sobre probabilidade de ocorrência de valores fora da especificação. A conversão do valor observado em múltiplos do desvio padrão mostra a distância relativa entre a média e os limites. Quanto maior o Z-score, menor a probabilidade de falhas. Esse cálculo auxilia na tomada de decisão, especialmente em processos críticos que exigem níveis específicos de confiabilidade. A comparação entre distribuição real e limites definidos também permite avaliar discrepâncias entre desempenho desejado e desempenho observado, identificando oportunidades de melhoria e otimizando controles internos.
A análise da capabilidade está diretamente ligada à avaliação do risco de produzir itens fora do limite. Ídices baixos indicam maior probabilidade de falhas e aumento de custos associados a retrabalho, sucata ou devoluções. Índices elevados demonstram robustez, estabilidade e capacidade de atender requisitos sem necessidade de ajustes frequentes. A compreensão da relação entre capabilidade e risco permite tomar decisões informadas sobre investimentos, manutenção, controle de processos, planejamento de produção e melhoria contínua.
A interpretação do risco deve considerar impacto financeiro, criticidade do produto, requisitos regulatórios, tolerâncias de projeto e exigências de clientes. Em indústrias altamente reguladas, o risco de não conformidade envolve consequências significativas, exigindo níveis elevados de capabilidade. A avaliação crítica das curvas, dos índices e das análises complementares permite compreender o comportamento global do processo e apoiar ações estratégicas.
A aplicação da capabilidade assume, na maior parte das situações industriais, que os dados seguem distribuição aproximadamente normal. Entretanto, muitos processos reais apresentam distribuições que diferem substancialmente da normalidade, especialmente quando os valores observados são influenciados por limites físicos, comportamentos assimétricos ou mecanismos de geração de dados que favorecem concentrações em determinadas regiões. Em processos químicos, bioquímicos, de envase, de reações dependentes de temperatura, tempos de residência, viscosidades, dimensões geométricas específicas ou fenômenos que se aproximam de limites inferiores naturais, ocorre frequentemente assimetria acentuada. Esse comportamento é também comum em processos logísticos e operacionais que lidam com tempos de ciclo ou tempos de atendimento, nos quais valores baixos tendem a ser mais comuns e a distribuição apresenta cauda longa para a direita. A avaliação de capabilidade nesse contexto exige abordagem robusta, pois o cálculo tradicional dos índices utiliza desvio padrão e média, que não representam adequadamente dados assimétricos.
A análise técnica da distribuição deve ser feita com rigor estatístico, utilizando ferramentas como gráficos de probabilidade, testes de aderência, análise de momentos, avaliação de curtose e assimetria e ferramentas de comparação entre distribuições teóricas e empíricas. Quando a distribuição não é compatível com a normal, aplica-se o conceito de transformação para normalidade, que visa ajustar matematicamente os dados de forma que o modelo estatístico possa ser utilizado com maior precisão. A transformação de Box-Cox é uma das mais aplicadas, pois permite ajustar a escala dos dados através de um expoente que minimiza a assimetria e aproxima a distribuição da forma normal. A transformação de Johnson, que utiliza funções logísticas e hiperbólicas, oferece alternativa mais flexível, especialmente em distribuições com comportamento mais complexo.
A escolha da transformação requer análise crítica e conhecimento do processo. Transformações devem ser interpretadas como ferramenta estatística, e não como manipulação indevida dos dados. A interpretação dos resultados transformados deve considerar se o comportamento físico do processo é compatível com a forma ajustada. Quando a transformação aproxima a distribuição da normalidade sem distorcer relações fundamentais, a capabilidade pode ser calculada com maior confiabilidade. Quando a transformação não produz ajuste adequado ou altera significativamente a interpretação física dos dados, métodos não paramétricos ou análises alternativas podem ser mais apropriados.
O sistema de Johnson utiliza três famílias de funções para transformar distribuições não normais em distribuições aproximadamente normais. Essa abordagem é especialmente útil em processos industriais complexos, nos quais a assimetria é acentuada e onde transformações simples não produzem ajuste adequado. O método identifica parâmetros que permitem transformar a distribuição real em uma forma ajustada que permite cálculo confiável da capabilidade. Esse sistema é particularmente adequado para processos que apresentam limites naturais, concentrações assimétricas ou caudas longas.
A transformação Box-Cox, por sua vez, utiliza expoente ajustável que modifica proporcionalmente todos os valores e reduz a assimetria. A escolha do parâmetro lambda requer análise cuidadosa para evitar sobreajuste. Quando aplicada corretamente, a transformação reduz a influência de extremos e melhora a interpretação estatística. Em processos industriais, Box-Cox é frequentemente utilizado em análises de capabilidade, validação de processos, estudos de setagem e avaliação de desempenho contínuo.
Alternativas aceitas incluem técnicas não paramétricas que não dependem da suposição de normalidade. Métodos baseados em percentis, distribuições empíricas e simulações permitem avaliar capabilidade quando a distribuição é intrinsecamente não normal. Essas abordagens são especialmente relevantes em indústrias de alta complexidade, nas quais dados apresentam comportamento multimodal ou não apresentam ajuste adequado a modelos teóricos.
A capabilidade influencia diretamente decisões estratégicas associadas a risco, confiabilidade e custos industriais. Índices altos representam processos robustos, previsíveis e com menor probabilidade de gerar não conformidades. Em contrapartida, índices baixos indicam risco elevado, exigindo abordagens estruturadas de investigação, correção e prevenção. A interpretação dos índices deve ser feita em conjunto com parâmetros operacionais, dados históricos e maturidade dos controles aplicados. Em indústrias sensíveis a falhas, como farmacêutica, aeroespacial, automotiva e alimentícia, níveis elevados de capabilidade representam condição mínima para sustentação da confiabilidade operacional.
O impacto sobre custos ocorre porque processos incapazes geram retrabalho, sucata, devoluções, perda de produtividade e necessidade de controles adicionais. A análise de capabilidade permite identificar pontos críticos do processo, orientar ações de priorização e estabelecer estratégias de contenção e prevenção. A confiabilidade operacional depende de processos com dispersão reduzida e centragem adequada. A integração da capabilidade com ferramentas de análise de falhas, como FMEA e estudos de risco, permite criar sistemas capazes de antecipar problemas e melhorar desempenho global.
A produtividade também está diretamente ligada à capabilidade. Processos estáveis e robustos exigem menos intervenção, geram maior previsibilidade e permitem otimização de recursos. Em ambientes competitivos, a capabilidade elevada torna-se vantagem estratégica, pois reduz variabilidade, minimiza custos e aumenta a confiabilidade do produto. A tomada de decisão baseada em capabilidade fortalece a governança industrial e promove cultura orientada por dados.
A capabilidade é ferramenta essencial para priorizar projetos de melhoria contínua. Processos com índices baixos indicam áreas críticas que demandam intervenção. A avaliação deve considerar impacto sobre o cliente, custo da não conformidade, criticidade regulatória e frequência de ocorrência. Processos com Cpk menor que 1 apresentam risco elevado e exigem ações imediatas. Processos com Cpk entre 1 e 1,33 apresentam oportunidade significativa de melhoria, enquanto processos com índices superiores podem ser monitorados para manutenção de desempenho.
A priorização deve considerar a relação entre curto e longo prazo. Quando Cp é adequado, mas Pp é insuficiente, é necessário investigar estabilidade, padronização e treinamento. Quando Cp é baixo, o problema está na variabilidade intrínseca e pode requerer revisão de parâmetros de projeto, métodos, equipamentos ou controle de matéria-prima. A capabilidade fornece critérios objetivos para classificar áreas que exigem intervenção, evitar desperdício de recursos e garantir foco nas causas reais.
Ferramentas como DMAIC, análise de valor, otimização de parâmetros e estudo de tolerâncias complementam a abordagem. A integração entre capabilidade e métodos de melhoria contínua fortalece a eficiência global e permite tomada de decisão consistente. A priorização baseada em dados reduz subjetividade, aumenta transparência e orienta investimento em áreas que realmente impactam desempenho.
A capabilidade desempenha papel central em programas de Seis Sigma e na gestão da qualidade. No ciclo DMAIC, o cálculo de Cpk e Ppk é utilizado para quantificar desempenho inicial e estabelecer metas para melhoria. Na fase de medição, os índices funcionam como indicadores que traduzem variabilidade e centragem em métricas claras. Na fase de análise, a comparação entre curto e longo prazo indica causas de variabilidade e permite identificar fatores críticos que afetam o processo. Na fase de melhoria, os índices permitem validar eficácia das ações implementadas. Na fase de controle, o monitoramento contínuo da capabilidade garante que os resultados sejam sustentados ao longo do tempo.
A integração com Controle Estatístico de Processo é natural, pois a estabilidade é pré-requisito para cálculo adequado dos índices de curto prazo. O CEP fornece evidências sobre presença de causas especiais, tendências e ciclos. A validação de processos também depende de índices adequados, especialmente em setores regulados. A capabilidade representa evidência quantitativa de que o processo opera consistentemente dentro dos limites requeridos e que é capaz de produzir resultados confiáveis. A gestão por qualidade utiliza a capabilidade como indicador chave para tomada de decisão e avaliação de desempenho.
A validação de processos exige demonstração de que o desempenho atende critérios estabelecidos. A capabilidade funciona como ferramenta quantitativa para confirmar se o processo, após qualificação de equipamentos, materiais e operadores, opera consistentemente dentro das tolerâncias estabelecidas. Em indústrias críticas, índices elevados são requeridos para assegurar segurança, eficácia e confiabilidade. O CEP complementa essa abordagem ao monitorar continuamente o processo e detectar desvios antes que se tornem problemas.
A integração da capabilidade com controle estatístico permite estabelecer sistemas robustos de governança. A interpretação dos índices fornece base para decisões como ajuste de parâmetros operacionais, calibração de instrumentos, revisão de procedimentos e implementação de ações preventivas. A validação contínua depende de análises estatísticas confiáveis e de entendimento profundo das fontes de variabilidade. A capabilidade integra esses elementos e permite abordagem sistemática para garantir desempenho operacional.
A capabilidade de processo representa ferramenta essencial para avaliação de desempenho, tomada de decisão industrial e gestão orientada por dados. A compreensão integrada das métricas Cp, Cpk, Pp e Ppk exige análise estatística robusta, conhecimento profundo do processo e interpretação alinhada ao contexto operacional e estratégico. O cálculo adequado dos índices depende de estabilidade, normalidade, representatividade das amostras e entendimento das diferenças entre curto e longo prazo. A interpretação exige considerar variabilidade, centragem, risco, criticidade e impacto financeiro. A capabilidade fortalece governança industrial, orienta priorização de melhorias, suporta validação de processos e promove cultura de dados capaz de sustentar competitividade e desempenho sustentável.
